计算机中数的表示
1、计算机中用二进制计数:
计算机是由数字电路搭成的,而数字电路只有1和0两种状态。所以对于计算机来说,使用二进制(Binary)是最自然的方式。二进制的一位数字叫做一个位(Bit),逢二进一,事实上计算机采用逻辑电路计算两个bit之间的加法。下图为一位全加器(1-bit FullAdder),电压值只有0和1两种状态,输入到门电路的输入端,经过相应的逻辑运算后通过输出端输出结果电压值。各种门电路对应着不同的逻辑运算。
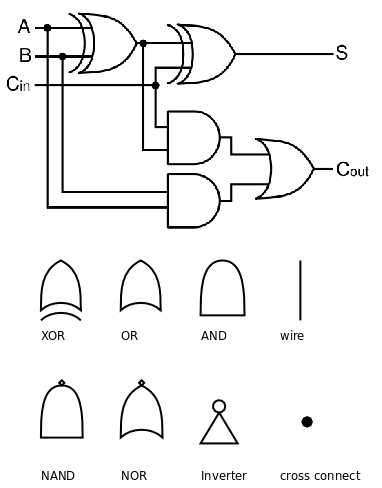
该图中主要使用了三种逻辑运算来实现两个bit的加法,分别为XOR(异或—相同为0,不相同为1)、AND(与)和OR(或)。
左上角为两个输入A和B,$C_{in}$是低位传来的进位(Carry),相当于三个加数A,B,$C_{in}$求和,三个加数都为0的话,最后的结果为0,三个加数都为1的话,最后的结果为11,即输出为S的结果是1代表了低位,产生的进位高位$C_{out}$也是1。S和$C_{out}$最后组成了两个bit相加的最后结果。所以可能的结果如下面的真值表所示:
| A | B | $C_{in}$ | $C_{out}$ | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
如果把很多给这样的1位全加器串联起来,就可以组成一个多位加法器。
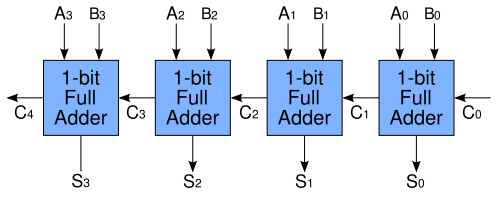
如上图所示,为一个4位全加器,这里将$C_{out}$作为下一级全加器的$C_{in}$,也就是在进行一步步的进位操作,可以称他为Ripple Carry Adder,通过这个全加器将两个4bit的二进制数$A_3A_2A_1A_0$和$B_3B_2B_1B_0$加起来。
2、不同进制的换算
二进制中换算为十进制:
下标2表示这个数是二进制数,对于二进制数$A_3A_2A_1A_0$来说,$A_3$称为最高位(MSB,Most Significant Bit),$A_0$称为最低位(LSB,Least Significant Bit)。在计算机中,按惯例,最低位LSB从0开始。
十进制转换为二进制一般使用除二反序取余法,也就是将需转换的十进制数除以2取余数,反复进行,一直到最后被除数为0或1时结束,将这些余数按照相反的顺序排序得到的数即为该二进制数对应的十进制数。
在实际中,一般使用8进制数或者16进制数,将二进制数分为每三位一组,每组用一个十进制数字(范围为$0-7$)来表示,这样的数逢八进一,称之为八进制数(Octal) 。如果将二进制数分为每四位一组,每组同样的用一个十进制数(范围($0-15$,大于9的数字用字母A开始表示,也就是用$A-F$表示10-15)来表示,这样的数逢十六进一 ,称之为十六进制数(Hexadecimal) 。
习题
1、二进制小数可以这样定义:
(0.A1A2A3…)2=A1×2-1+A2×2-2+A3×2-3+…
这个定义同时也是从二进制小数到十进制小数的换算公式。从本节讲的十进制转二进制的推导过程出发类比一下,十进制小数换算成二进制小数应该怎么算?
答:十进制小数的小数部分乘以2,取整数部分依次放在小数点之后,知道小数点后的数为0.
3、整数的加减运算
Sign and Magnitude 表示法:
要用8个bit表示正数和负数,一种简单的想法是把最高位规定为符号位(Sign Bit),0表示正1表示负,剩下的7位表示绝对值的大小,这称为Sign and Magnitude表示法。 这样用8个bit表示整数的取值范围是$-2^7-1 2^7-1$,即-127~127。
在这种表示法中,计算机做加法运算需要处理以下逻辑:
- 如果两数符号位相同,就把它们的低7位相加,符号位不变。如果低7位相加时在最高位产生进位,说明结果的绝对值大于127,超出7位所能表示的数值范围,这称为溢出(Overflow)[24],这时通常把计算机中的一个标志位置1表示当前运算产生了溢出。
- 如果两数符号位不同,首先比较它们的低7位谁大,然后用大数减小数,结果的符号位和大数相同。
1‘s Complement表示法:
这是一种二进制补码表示法。
| 数值 | 补码表示 |
|---|---|
| -499 | 500 |
| -498 | 501 |
| … | … |
| -1 | 998 |
| 0 | 999 |
| 0 | 0 |
| 1 | 1 |
| … | … |
| 498 | 498 |
| 499 | 499 |
十进制中,负数用9的补码表示,减法转换成加法,计算结果的最高位如果有进位则要加回到最低位上去。要验证这条规则得考虑四种情况:
- 两个正数,相加得正
- 一正一负,相加得正
- 一正一负,相加得负
- 两个负数,相加得负
二进制中,负数用1的补码(1’s Complement)表示,减法转换成加法,计算结果的最高位如果有进位则要加回到最低位上去。 取1的补码就是把每个bit取反,所以1的补码也称为反码。 该方法对于符号表示法来说,不需要吧符号和绝对值分开考虑,正负数的加法都一样。如果8个bit采用1’s Complement表示法,负数的取值范围是从10000000到11111111(-127到0),正数是从00000000到01111111(0到127),仍然可以根据最高位判断一个数是正是负。美中不足的是0的表示仍然不唯一,既可以表示成11111111也可以表示成00000000,为了解决这最后一个问题,我们引入2’s Complement表示法。
2’s Complement表示法:
正数不变,负数先取反码再加1。如果8个bit采用2’s Complement表示法,负数的取值范围是从10000000到11111111(-128到-1),正数是从00000000到01111111(0到127),也可以根据最高位判断一个数是正是负,并且0的表示是唯一的,目前绝大多数计算机都采用这种表示法。 减法转换成加法,忽略计算结果最高位的进位,不必加回到最低位上去。 8个bit采用2’s Complement表示法的取值范围是-128~127 。
如果两个正数相加溢出,结果一定是负数;如果两个负数相加溢出,结果一定是正数;一正一负相加,无论结果是正是负都不可能溢出。

在相加过程中最高位产生的进位和次高位产生的进位如果相同则没有溢出,如果不同则表示有溢出。
4、有符号数和无符号数
用8个bit表示正数和负数,这些数称为有符号数(Signed Number );如果8个bit全部表示正数则取值范围是0~255,这称为无符号数(Unsigned Number)。
计算机的加法器在做完计算之后,根据最高位产生的进位设置进位标志,同时根据最高位和次高位产生的进位的异或设置溢出标志。 如果计算结果的所有bit都是零则设置零标志,如果计算结果的最高位是1则设置负数标志,如果程序把计算结果理解成有符号数,也可以检查负数标志判断结果是正是负。
5、浮点数
浮点数在计算机中的表示是基于科学计数法(Scientific Notation)的,我们知道32767这个数用科学计数法可以写成$3.2767×10^4$,3.2767称为尾数(Mantissa,或者叫Significand),4称为指数(Exponent)。浮点数在计算机中的表示与此类似,只不过基数(Radix)是2而不是10。 在这里浮点数由三个部分组成:符号位、指数部分(表示2的多少次方)和尾数部分(小数点前面是0,尾数部分只表示小数点后的数字) :

使用这个方法表示负数时,我们可以在指数部分规定一个符号位,然而更广泛采用的办法是使用偏移的指数(Biased Exponent)。规定一个偏移值,比如16,实际的指数要加上这个偏移值再填写到指数部分,这样比16大的就表示正指数,比16小的就表示负指数。
每个浮点数的表示都不唯一,例如$17=(0.10001)_2×2^5=(0.010001)_2×2^6$,这样给计算机处理增加了复杂性。为了解决这个问题,我们规定尾数部分的最高位必须是1,也就是说尾数必须以0.1开头,对指数做相应的调整,这称为正规化(Normalize)。由于尾数部分的最高位必须是1,这个1就不必保存了,可以节省出一位来用于提高精度,我们说最高位的1是隐含的(Implied)。
做浮点运算时要注意精度损失(Significance Loss)问题,有时计算顺序不同也会导致不同的结果。